2 분 소요

seq2seq(Sequence-to-Sequence)

스크린샷 2023-08-29 오후 4.12.33

공부 정리에 앞서 서울대 데이터사이언스학과 이준석 교수님의 강의 자료를 이용했다는 점을 명시합니다!

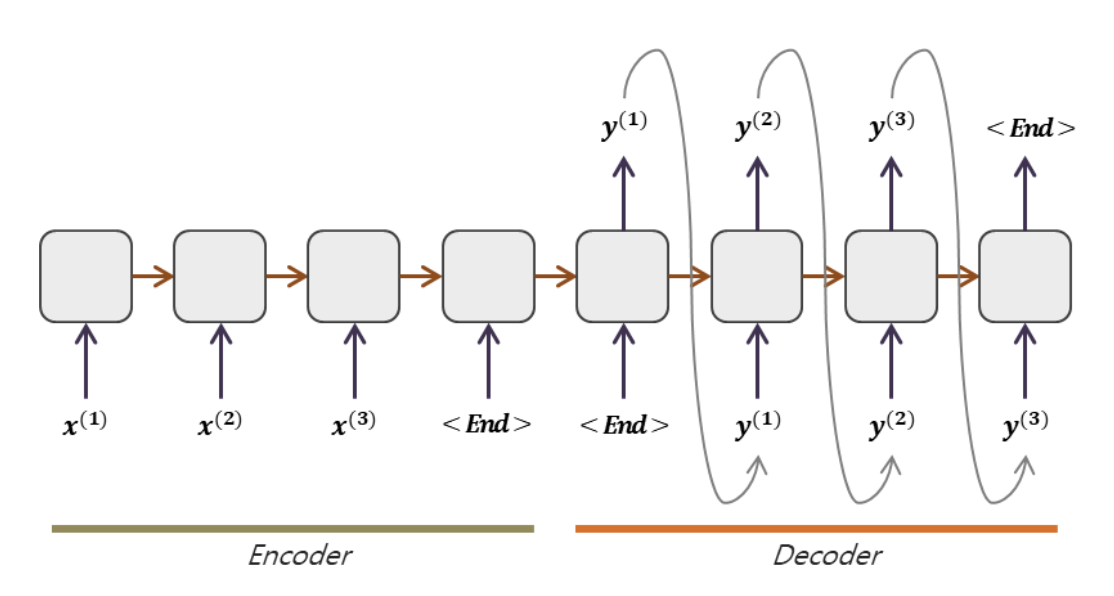
Machine Translation 기술이 크게 발전하기 이전에, 연구자들은 이전에 가지고 있던 RNN구조를 통해서 input의 하나의 토큰과 output의 하나의 토큰을 matching 시키는 방식으로 translation을 진행시키면 된다고 생각했다. 하지만, 각 나라의 언어들은 경우에 따라 문법도 다르고, 한 단어를 표현하는 길이도 다르고 심지어 문장 순서도 다르다. 모든 언어들이 1대1 매칭이 될 수 없다는 것이다. 즉, 이전의 Many to Many 문제를 해결하는 RNN구조는 1대1 matching에 크게 의존했다. 이러한 문제점을 해결하고자 seq2seq라는 새로운 방법이 제시되었다.

우선 input으로 들어온 모든 문장을 output을 내지 않고 다 읽어야 된다는 것이 seq2seq의 입장이다. seq2seq는 크게 Encoder, Decoder 구조로 이루어져 있다. Encoder에서는 input으로 들어온 문장을 단위별로 쭉 읽으며 hidden state에 정보를 저장하고 모든 문장의 정보가 압축되기를 기대하며 하나의 context vector안에 정보를 압축한다. 압축한 context vector를 가지고 Decoder의 첫입력을 받는다. 이때 Decoder는 context vector를 활용해 첫 output을 내고 이 output을 다음 step의 input값으로 자동으로 받아 hidden state와 함께 다음 step의 output을 내고 EOS(End Of Sentence)가 나올때까지 반복해서 위의 과정을 진행한다. 이를 Auto-Regressive한 방식이라고 한다.

하지만 이러한 seq2seq방식에는 큰 문제점이 있었다. Decoder는 Encoder에서 나온 모든 정보를 이용하지 못하고 단지 압축되어 있는 단 하나의 context vector만을 이용해서 output을 내야 했기에, input data의 크기가 엄청 커지거나 정보량이 많아지면 context vector만으로는 방대한 정보량을 모두 담지 못해 좋지 못한 quality의 output값이 도출된다는 점이다. 따라서 연구자들은 Encoder과정에서 나온 hidden state를 decoding과정에서 매 step마다 이용해주면 훨씬 좋은 결과를 도출할 수 있을 것 같다는 생각을 하였고 이 생각에서 나온 mechanism이 바로 attention기법이다!

Attention

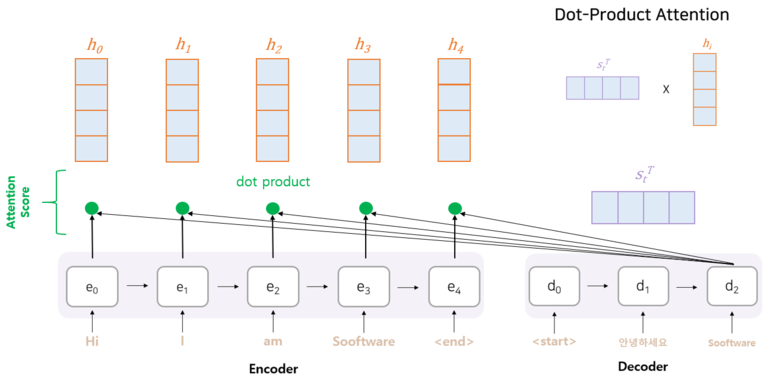
attention_seq2seq

RNN의 hidden state는 dimension이 지정되어있어 input값이 커진다면 input에 대한 정보를 hidden state에 모두 담을 수 없다는 문제가 있다. 또한 decoding과정에서 압축된 hidden state만을 가지고 output을 내려다 보니 좋지 않은 결과가 나오고 모든 step의 hidden state를 참조하지 못한다는 점이 있었다. 이러한 문제점을 해결하고자 attention기법이 사용되었다.

Attention 기법은 크게 보자면 Encoder의 모든 hidden state를 참고하여 decoder가 output을 도출하는 방법이라고 보면 된다. 이때, decoder의 현 시점의 hidden state와 encoder의 모든 hidden state들과의 dot product(내적)을 수행하여 attention score를 구한 후, attention score에 따른 중요도를 가지고 output 결과를 도출하는 것이다.

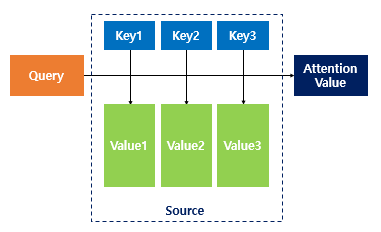
attention

Attention Function: Attention(Query, Key, Value) = Attention Value

우선 Key와 Value는 하나의 pair로 이루어져 있다. Key-Value pair에서 본체가 Value이고 이를 변호하는 역할이 Key라고 생각하면 쉽다. Attention Value는 Key-Value pair의 모든 Value들과 Weight간의 곱을 통해서 도출되는데 해당 Value에 얼만큼의 Weight를 곱해줘야 하냐를 결정하는 역할을 Query와 Key가 담당한다. Query는 Key들에 대해 얼마만큼 연관성이 있는 지 모두 비교해보면서 해당 Key의 Value에 얼마만큼의 Weight를 참여시킬지 정하는 역할을 한다고 보면 쉽다.

seq2seq를 예시로 들자면, Query는 Decoder의 hidden state에 해당하고, Key와 Value는 모든 step의 Encoder hidden state에 해당한다. Key와 Value는 mapping이 되어있는 관계이지만 경우에 따라 Key와 Value값을 동일하게 설정하는 경우도 있다고 한다.

Query와 Key는 서로 Similarity 비교를 해야하므로 dimension이 같아야 한다. 또한 Value와 Weight를 통한 곱과 합을 통해 Attention Value를 나타내기에 Value와 Attention Value의 dimension 역시 같아야 한다. 실제로는 Query, Key, Value, Attnetion Value 모두 dimension이 같은 모델들이 많다고 한다.

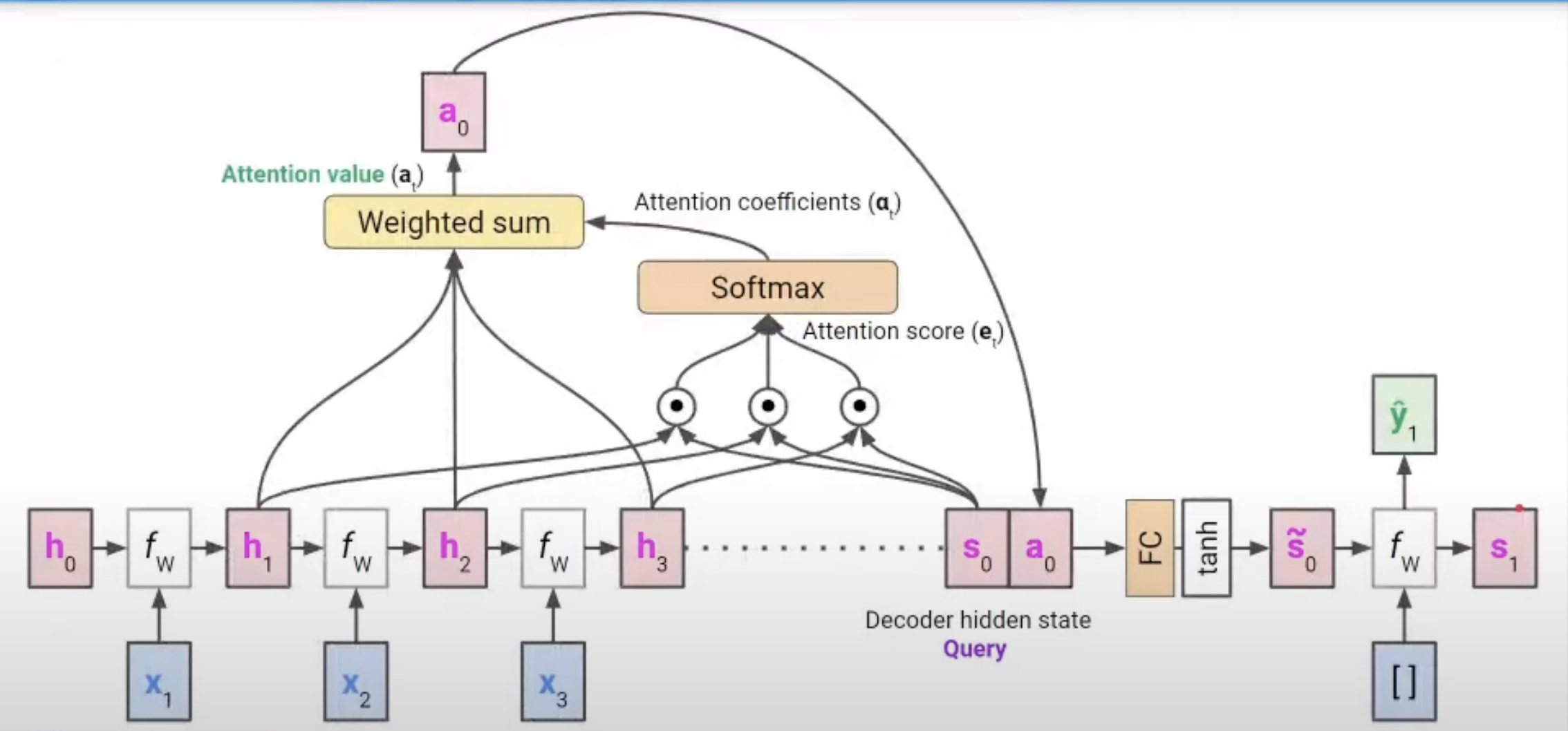
attention_full

​   Encoder hidden states: $h_1, \dots, h_T \in \mathbb{R}^h$

  1. Decoder의 hidden state와 Encoder의 모든 hidden state 간의 내적을 통해 Attention score를 구한다.
    $e_t = [s_t^T \circ h_1, s_t^T \circ h_2, \dots , s_t^T \circ h_T] \in \mathbb{R}^T $ (t는 현재 decoder의 step)

  2. 지저분한 숫자로 이루어져 있을 Attention Score를 Normalize하기 위해 Softmax 함수를 통해 Attention Coefficients를 구한다.
    $\alpha_t = Softmax(e_t) \in \mathbb{R}^T$

  3. Attention Coefficients와 encoder hidden state의 Value값들 간의 Weighted Sum을 통해 Attention Value를 구한다.
    $a_t = \sum_{i=1}^T [\alpha_t]_i h_i \in \mathbb{R}^h$

  4. 구한 Attention Value를 현재 step의 decoder hidden state와 concatenate한다.
    $[a_t;s_t] \in \mathbb{R}^{2h}$

  5. Decoder의 hidden state의 dimension은 $ \mathbb{R}^h $이기에 차원축소를 위해 FC layer와 tanh를 거쳐서 hidden state $\tilde{s_t}$를 만든다.
    $\tilde{s_t} \in \mathbb{R}^h$

  6. Hidden state $\tilde{s_t}$를 통해 output $y_t$를 구하고 output과 hidden state를 통해 계속해서 EOS전까지 output값을 도출한다. 이때, 매 step마다 hidden state값을 구하기 위해 5번과정을 수행한다.

참고