2 분 소요

LSTM(Long Short Term Memory)

RNN(Recurrent Neural Network)은 이전정보를 기억하며 네트워크를 계속해서 학습시키는 모델로 시계열 데이터에 큰 강점을 지닌 모델이다. 이전 step에서의 정보 $h_{t-1}$과 현재 step에서의 입력 값 $x_t$를 입력으로 받아 모델에 넣어주면 $h_t$가 도출되고 이를 다음 step에 이용하며 계속해서 다음 step으로 전달하여 연산하는 방식이다. 그래서 time-series data 처리에 큰 강점을 가지고 있다.

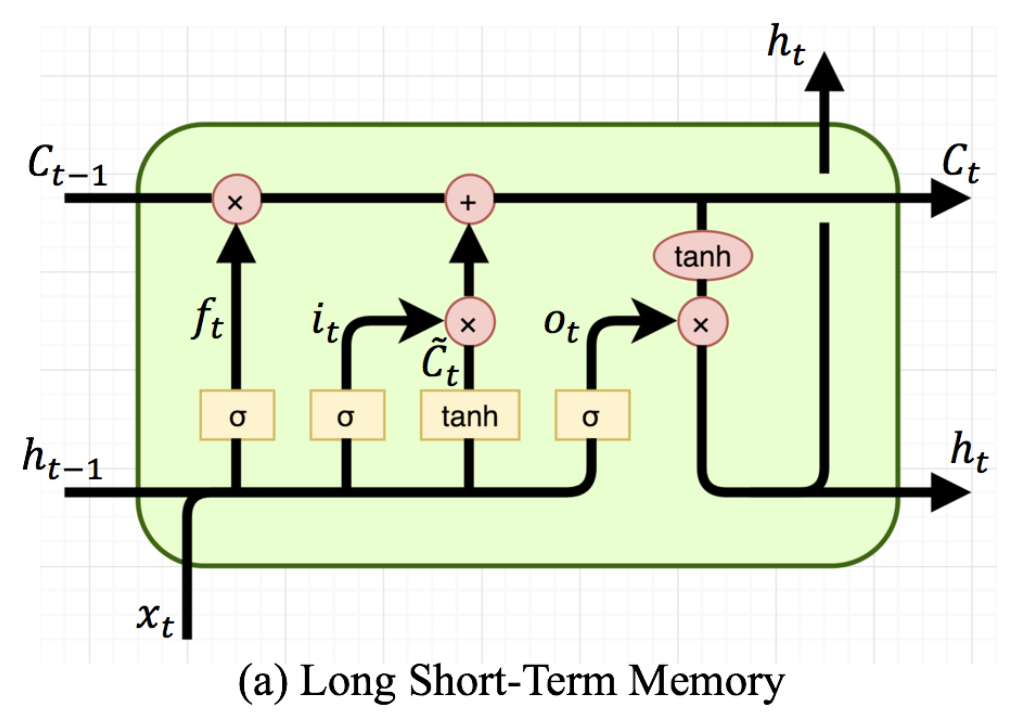
하지만, RNN에서 Back-Propagation을 통해 weight를 update할 경우, time step t가 일정이상으로 커지면 최종 time step T부터 0까지 미분을 진행하며 BackPropagation이 진행되기에 기울기 소실(Gradient Vanishing) 문제가 발생한다. 즉, 비교적 빠른 time step에 대한 정보가 고려되지 않는 문제가 발생한다. 이를 해결하기 위해 RNN보다는 좀 더 복잡한 방식으로 구성되어 있는 LSTM이 제안되었다. LSTM은 은닉층의 메모리 셀에 Input Gate, Forget Gate, Output Gate를 추가하여 불필요한 기억을 지우고, 기억해야할 것들을 정한다. 요약하면 LSTM은 hidden state를 계산하는 식이 전통적인 RNN보다 조금 더 복잡해졌으며 cell state라는 값을 추가하였다.

LSTM

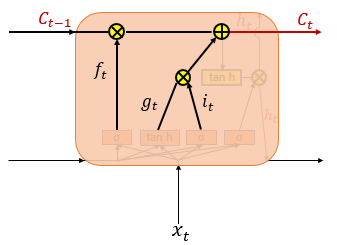
Cell State

Cell state

Cell state는 LSTM에서 추가된 또다른 hidden state라고 봐도 무방하다. Cell state는 RNN에서 발생한 gradient vanishing을 해결하는 중요한 역할을 담당한다. Cell state 역시 hidden state와 마찬가지로 이전 step의 결과를 다음 step의 입력값으로 넣어준다. Cell state의 주된 역할을 LSTM에 존재하는 Gate들과 상호작용하며 선택적으로 정보를 활용한다는 점이다. Cell State의 값은 Input Gate, Forget Gate의 값들을 이용하여 구하게 되는데 식은 다음과 같다. $f_t$는 Forget Gate에서 도출된 값이고 $i_t, g_t$는 Input Gate에서 도출된 값이다.

$c_t = f_t \otimes c_{t-1} + i_t \otimes g_t$

Input Gate

  • 현재 정보를 잊거나 기억하기 위한 Gate

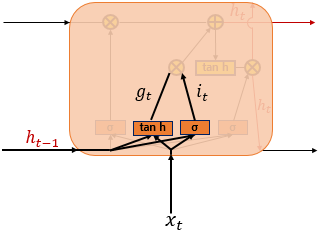
Input Gate

$i_t = \sigma(W_{xi}x_t + W_{hi}h_{t-1} + b_i)$
$g_t = tanh(W_{xg}x_t + W_{hg}h_{t-1} + b_g)$

둘 다 모두 이전 시점의 $h_{t-1}$과 현재 시점 $x_t$를 이용하여 연산을 하는 것을 알 수 있다.
$i_t$는 sigmoid함수를 이용하여 범위를 0 < $i_t$ < 1로 설정하였으며 이는 0에 가까울 수록 많은 정보를 삭제하고 1에 가까울 수록 많은 정보를 기억한다고 보면 된다.
$g_t$는 tanh함수를 이용하여 범위를 -1 < $g_t$ < 1로 설정하여 나중에 현재 정보를 얼마나 더할 것인지를 결정한다.

Forget Gate

  • 과거 정보를 잊거나 기억하기 위한 Gate

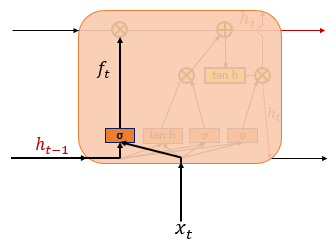
forgetgate

$f_t = \sigma(W_{xf}x_t + W_{hf}h_{t-1} + b_f)$

시그모이드 함수를 지나면 0과 1 사이의 값이 나오게 되는데, 이 값이 곧 삭제 과정을 거친 정보의 양이다. 0에 가까울수록 정보가 많이 삭제된 것이고 1에 가까울수록 정보를 온전히 기억한 것이다.

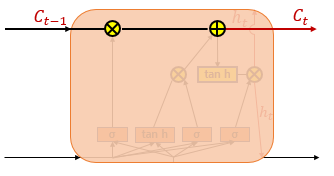
Cell State Update

Cell_state

$C_t = f_t \circ C_{t-1} + i_t \circ g_t $

위의 식에서 알 수 있듯이 $f_t$의 값이 0에 가까우면 이전 상태의 Cell state를 거의 반영하지 않고 1에 가까우면 많이 반영한다는 점을 알 수 있다. 또한 입력 게이트의 $i_t$값이 0에 가까우면 현재 상태의 값을 거의 반영하지 않고 1에 가까우면 현재 상태의 값을 많이 반영한다는 점을 알 수 있다. 결과적으로 삭제 게이트는 이전 시점의 입력을 얼마나 반영할지를 의미하고, 입력 게이트는 현재 시점의 입력을 얼마나 반영할지를 결정한다.

Output state and Hidden state

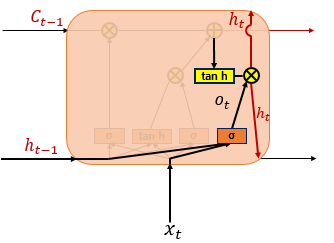
OutputGate

$o_t = \sigma(W_{xo}x_t + W_{ho}h_{t-1} + b_o)$
$h_t = o_t \circ tanh(c_t)$

현시점의 hidden state는 cell state와 함께 계산이 되며, 출력이 되는 동시에 다음 시점으로 hidden state가 이용된다.

LSTM의 너무 복잡한 구조로 인해 자연어처리의 대가 조경현 교수님께서 제안하신 GRU라는 모델 역시 큰 각광을 받았다. 여전히 두 모델은 큰 주축이 되고 있는 모델이다.

참고